User Interface
Basis functions
Gaussian type orbitals (GTO)
PyQInt uses cartesian Gaussian type orbitals as given by
wherein \(\alpha\) is the exponent, \(\vec{R} = \left(X,Y,Z\right)\) the position of the orbital, \((l,m,n)\) the orders of the pre-exponential polynomial, and \(N\) a normalization constant such that
Note
The normalization constant is automatically calculated by PyQInt based on the value of \(\alpha\) and \((l,m,n)\) and does not have to be supplied by the user.
GTOs are a fundamental building block of CGF (see below) and typically a user would not directly work with them. Nevertheless, GTO objects can be constructed as follows:
from pyqint import PyQInt, cgf, gto
coeff = 1.0 # coefficients only have meaning for GTOs within a CGF
alpha = 0.5
l,m,n = 0,0,0
p = (0,0,0)
G = gto(coeff, p, alpha, l, m, n)
Note
If you work with individual GTOs, the first parameter to construct the GTO should have a value of 1.0. This first parameter corresponds to the linear expansion coefficient used in the formulation of Contracted Gaussian Functions (see below).
Contracted Gaussian Functions (CGF)
Several GTOs can be combined to produce a so-called Contracted Gaussian Functional which is esentially a linear combination of GTOs as given by
To build a CGF, we first have to produce the CGF object and then add GTOs to it:
from pyqint import PyQInt, cgf
cgf = cgf([0.0, 0.0, 0.0])
cgf.add_gto(0.154329, 3.425251, 0, 0, 0)
cgf.add_gto(0.535328, 0.623914, 0, 0, 0)
cgf.add_gto(0.444635, 0.168855, 0, 0, 0)
Note
The first argument of the add_gto function is the linear expansion coefficient
\(c_{i}\) and the second argument is \(\alpha\).
Integral evaluation
Electronic structure calculations require the construction of molecular integrals. Here, an overview is given of the integrals involved and how these can be evaluated using PyQInt.
Overlap integrals
Overlap integrals effectively probe the overlap between two CGFs and are given by
CGFs should be normalized and as such, their self-overlap should be equal to 1. In the code snippet below, the overlap matrix \(\mathbf{S}\) is calculated for a basis set composed of the two \(1s\) atomic orbitals on H which are separated by a distance of 1.4 Bohr.
from pyqint import PyQInt, cgf
import numpy as np
from copy import deepcopy
# construct integrator object
integrator = PyQInt()
# build CGF for a H atom located at the origin
cgf1 = cgf([0.0, 0.0, 0.0])
cgf1.add_gto(0.154329, 3.425251, 0, 0, 0)
cgf1.add_gto(0.535328, 0.623914, 0, 0, 0)
cgf1.add_gto(0.444635, 0.168855, 0, 0, 0)
# create a copy of the CGF located 1.4 a.u. separated from CGF1
cgf2 = deepcopy(cgf1)
cgf2.p[2] = 1.4
# construct empty matrix
S = np.zeros((2,2))
S[0,0] = integrator.overlap(cgf1, cgf1)
S[0,1] = S[1,0] = integrator.overlap(cgf1, cgf2)
S[1,1] = integrator.overlap(cgf2, cgf2)
# output result
print(S)
The result of this script is:
[[1.00000011 0.6593185 ]
[0.6593185 1.00000011]]
Kinetic integrals
Kinetic integrals determine the kinetic energy of a given orbital and are given by
In the code snippet below, the kinetic energy matrix \(\mathbf{T}\) is calculated for a basis set composed of the two \(1s\) atomic orbitals on H which are separated by a distance of 1.4 Bohr.
from pyqint import PyQInt, cgf, gto
import numpy as np
from copy import deepcopy
# construct integrator object
integrator = PyQInt()
# build CGF for a H atom located at the origin
cgf1 = cgf([0.0, 0.0, 0.0])
cgf1.add_gto(0.154329, 3.425251, 0, 0, 0)
cgf1.add_gto(0.535328, 0.623914, 0, 0, 0)
cgf1.add_gto(0.444635, 0.168855, 0, 0, 0)
# create a copy of the CGF located 1.4 a.u. separated from CGF1
cgf2 = deepcopy(cgf1)
cgf2.p[2] = 1.4
# construct empty matrix
T = np.zeros((2,2))
T[0,0] = integrator.kinetic(cgf1, cgf1)
T[0,1] = T[1,0] = integrator.kinetic(cgf1, cgf2)
T[1,1] = integrator.kinetic(cgf2, cgf2)
# output result
print(T)
The result of the above script is:
[[0.76003161 0.23645446]
[0.23645446 0.76003161]]
Nuclear attraction integrals
Nuclear attraction integrals determine the attraction between a given nucleus and the atomic orbital and are given by
In the code snippet below, the nuclear attraction energy matrices \(\mathbf{V}_{1}\) and \(\mathbf{V}_{2}\) are calculated for a basis set composed of the two \(1s\) atomic orbitals on H which are separated by a distance of 1.4 Bohr. Due to the symmetry of the system, the nuclear attraction matrices for each of the nuclei are the same.
from pyqint import PyQInt, cgf, gto
import numpy as np
from copy import deepcopy
# construct integrator object
integrator = PyQInt()
# build CGF for a H atom located at the origin
cgf1 = cgf([0.0, 0.0, 0.0])
cgf1.add_gto(0.154329, 3.425251, 0, 0, 0)
cgf1.add_gto(0.535328, 0.623914, 0, 0, 0)
cgf1.add_gto(0.444635, 0.168855, 0, 0, 0)
# create a copy of the CGF located 1.4 a.u. separated from CGF1
cgf2 = deepcopy(cgf1)
cgf2.p[2] = 1.4
# Build nuclear attraction integrals
V1 = np.zeros((2,2))
V1[0,0] = integrator.nuclear(cgf1, cgf1, cgf1.p, 1)
V1[0,1] = V1[1,0] = integrator.nuclear(cgf1, cgf2, cgf1.p, 1)
V1[1,1] = integrator.nuclear(cgf2, cgf2, cgf1.p, 1)
V2 = np.zeros((2,2))
V2[0,0] = integrator.nuclear(cgf1, cgf1, cgf2.p, 1)
V2[0,1] = V2[1,0] = integrator.nuclear(cgf1, cgf2, cgf2.p, 1)
V2[1,1] = integrator.nuclear(cgf2, cgf2, cgf2.p, 1)
# print result
print(V1)
print(V2)
The result of the above script is:
[[-1.22661358 -0.59741732]
[-0.59741732 -0.6538271 ]]
[[-0.6538271 -0.59741732]
[-0.59741732 -1.22661358]]
Two-electron integrals
Two electron integrals capture electron-electron interactions, specifically electron-electron repulsion and electron exchange. They are defined as
The two-electron integrals are the most expensive terms to calculate in any electronic structure calculation due to their \(N^{4}\) scaling where \(N\) is the number of basis functions.
Note
PyQInt offers a separate routine for the efficient evaluation of all the integrals including the two electron integrals.
Although there are essentially \(N^{4}\) different two-electron integrals, due to certain symmetries the number of unique two-electron integrals is smaller. In the script below, the six unique two-electron integrals for the H2 system are calculated.
from pyqint import PyQInt, cgf, gto
import numpy as np
from copy import deepcopy
# construct integrator object
integrator = PyQInt()
# build CGF for a H atom located at the origin
cgf1 = cgf([0.0, 0.0, 0.0])
cgf1.add_gto(0.154329, 3.425251, 0, 0, 0)
cgf1.add_gto(0.535328, 0.623914, 0, 0, 0)
cgf1.add_gto(0.444635, 0.168855, 0, 0, 0)
# create a copy of the CGF located 1.4 a.u. separated from CGF1
cgf2 = deepcopy(cgf1)
cgf2.p[2] = 1.4
T1111 = integrator.repulsion(cgf1, cgf1, cgf1, cgf1)
T1122 = integrator.repulsion(cgf1, cgf1, cgf2, cgf2)
T1112 = integrator.repulsion(cgf1, cgf1, cgf1, cgf2)
T2121 = integrator.repulsion(cgf2, cgf1, cgf2, cgf1)
T1222 = integrator.repulsion(cgf1, cgf2, cgf2, cgf2)
T2211 = integrator.repulsion(cgf2, cgf2, cgf1, cgf1)
print(T1111)
print(T1122)
print(T1112)
print(T2121)
print(T1222)
print(T2211)
The output of the above script is given by:
0.7746057639733748
0.5696758530951017
0.44410766568798127
0.29702859983423036
0.4441076656879813
0.5696758530951017
Dipole-moment integrals
Dipole-moment integrals are defined as
and are evaluated with respect to the coordinate center of the system. Dipole moments are vector quantities, but in this implementation the dipoles are evaluated in the \(x\), \(y\), \(z\) separately.
In the script below, the dipole integrals are evaluated for the H2O
molecule using a sto3g basis set and in each cartesian direction. The result
is collected in a three-dimensional array.
from pyqint import PyQInt, Molecule
import numpy as np
# construct integrator object
integrator = PyQInt()
# build water molecule
mol = Molecule("H2O")
mol.add_atom('O', 0.00000, -0.07579, 0.0000, unit='angstrom')
mol.add_atom('H', 0.86681, 0.60144, 0.0000, unit='angstrom')
mol.add_atom('H', -0.86681, 0.60144, 0.0000, unit='angstrom')
cgfs, nuclei = mol.build_basis('sto3g')
N = len(cgfs)
D = np.zeros((N,N,3))
for i in range(N):
for j in range(i,N):
for k in range(0,3): # loop over directions
D[i,j,k] = integrator.dipole(cgfs[i], cgfs[j], k)
print(D)
The result of the above script is:
[[[ 0.00000000e+00 -1.43222417e-01 0.00000000e+00]
[ 0.00000000e+00 -3.39013356e-02 0.00000000e+00]
[ 5.07919476e-02 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 5.07919476e-02 0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00 5.07919476e-02]
[ 2.22964944e-03 -3.75854187e-03 0.00000000e+00]
[-2.22964944e-03 -3.75854187e-03 0.00000000e+00]]
[[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 -1.43222278e-01 0.00000000e+00]
[ 6.41172506e-01 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 6.41172506e-01 0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00 6.41172506e-01]
[ 2.62741706e-01 1.49973767e-01 0.00000000e+00]
[-2.62741706e-01 1.49973767e-01 0.00000000e+00]]
[[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 -1.43222278e-01 0.00000000e+00]
[-9.08620418e-18 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 4.37629746e-01 1.08953250e-01 0.00000000e+00]
[ 4.37629746e-01 -1.08953250e-01 0.00000000e+00]]
[[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 -1.43222278e-01 0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00 -9.08620418e-18]
[ 1.47399486e-01 3.34092154e-01 0.00000000e+00]
[-1.47399486e-01 3.34092154e-01 0.00000000e+00]]
[[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 -1.43222278e-01 0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00 2.48968067e-01]
[ 0.00000000e+00 0.00000000e+00 2.48968067e-01]]
[[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 1.63803356e+00 1.13655692e+00 0.00000000e+00]
[-1.38777878e-17 2.06582174e-01 0.00000000e+00]]
[[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[-1.63803356e+00 1.13655692e+00 0.00000000e+00]]]
Note
Each row in the above output corresponds to the dipole moment vector. There are in total 7 blocks to be observed and each block contains 7 rows. Each block corresponds to a different basis function in the bra and each row inside a block loops over the different basis functions in the ket.
Basis sets and molecules
Building molecules
Molecules can be efficiently built from the Molecule class. For example,
to build the H2 molecule, one can run the script below.
from pyqint import PyQInt, Molecule
import numpy as np
# construct integrator object
integrator = PyQInt()
# build hydrogen molecule
mol = Molecule('H2')
mol.add_atom('H', 0.0, 0.0, 0.0)
mol.add_atom('H', 0.0, 0.0, 1.4)
print(mol)
The output of the above script is:
Molecule: H2
H (0.000000,0.000000,0.000000)
H (0.000000,0.000000,1.400000)
Using the MoleculeBuilder class
Next to constructing molecules from scratch, one can also use the
MoleculeBuilder class which contains a number of pre-generated molecules.
The following molecules are available:
benzene
bf3
ch4
co
co2
ethylene
h2
h2o
he
lih
nh3
To load any of these molecules, one uses the from_name function
as shown in the script below
from pyqint import MoleculeBuilder
mol = MoleculeBuilder().from_name('ch4')
mol.name = 'CH4'
print(mol)
The output of the above script shows the elements and the atom positions:
Molecule: CH4
C (0.000000,0.000000,0.000000)
H (1.195756,1.195756,1.195756)
H (-1.195756,-1.195756,1.195756)
H (-1.195756,1.195756,-1.195756)
H (1.195756,-1.195756,-1.195756)
Note
Naming a molecule is completely optional and has no further implications
on any of the calculations. To name a molecule, populate the name
member of the Molecule class.
Alternatively, one can load molecules from a .xyz file via the
from_file routine.
mol = MoleculeBuilder().from_file('ch4.xyz')
Warning
It is assumed that the positions inside the .xyz file are stored in
angstroms. Internally, PyQInt uses Bohr distances and the
distances as reported in the .xyz file are automatically converted.
Constructing basis functions for a molecule
To construct the basis functions for a given molecule, one first needs to
construct the molecule after which the build_basis function can be used
to construct a basis.
The following basis sets are supported. For each basis set, the range of atoms that are supported are given:
sto3g(H-I)sto6g(H-Kr)p321(H-Cs)p631(H-Zn)
The example code below builds the basis functions for the H2 molecule:
from pyqint import PyQInt, Molecule
import numpy as np
# construct integrator object
integrator = PyQInt()
# build hydrogen molecule
mol = Molecule('H2')
mol.add_atom('H', 0.0, 0.0, 0.0)
mol.add_atom('H', 0.0, 0.0, 1.4)
cgfs, nuclei = mol.build_basis('sto3g')
for cgf in cgfs:
print(cgfs)
for nucleus in nuclei:
print(nucleus)
The output of the above script is:
[<pyqint.cgf.cgf object at 0x000001BDEDB37430>, <pyqint.cgf.cgf object at 0x000001BDEDB37F10>]
[<pyqint.cgf.cgf object at 0x000001BDEDB37430>, <pyqint.cgf.cgf object at 0x000001BDEDB37F10>]
[array([0., 0., 0.]), 1]
[array([0. , 0. , 1.4]), 1]
Parallel evaluation of integrals
From a collection of Contracted Gaussian Functions, the complete set of overlap, kinetic, nuclear attraction and two-electron integrals can be quickly evaluated using the build_integrals_openmp function. The function will automatically determine the number of available cores to allocate for this process.
from pyqint import PyQInt, Molecule
import numpy as np
# construct integrator object
integrator = PyQInt()
# build hydrogen molecule
mol = Molecule()
mol.add_atom('H', 0.0, 0.0, 0.0)
mol.add_atom('H', 0.0, 0.0, 1.4)
cgfs, nuclei = mol.build_basis('sto3g')
# evaluate all integrals
S, T, V, teint = integrator.build_integrals_openmp(cgfs, nuclei)
print(S)
print(T)
print(V)
print(teint)
The output of the above script is given by:
[[1.00000011 0.6593185 ]
[0.6593185 1.00000011]]
[[0.76003161 0.23645446]
[0.23645446 0.76003161]]
[[-1.88044067 -1.19483464]
[-1.19483464 -1.88044067]]
[0.7746057639733748, 0.4441076656879813, 0.29702859983423036, 0.5696758530951017, 0.44410766568798105, 0.7746057639733748]
Electronic structure calculations
Hartree-Fock
The Hartree-Fock procedure is readily available as a separate class in the PyQInt package. It gives rich output allowing the user to investigate the Hartree-Fock coefficient optimization procedure in detail.
from pyqint import PyQInt, Molecule, HF
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import make_axes_locatable
def main():
# calculate sto3g coefficients for h2o
cgfs, coeff = calculate_co()
# visualize orbitals
fig, ax = plt.subplots(2,3, figsize=(18,10))
for i in range(0,2):
for j in range(0,3):
dens = plot_wavefunction(cgfs, coeff[:,i*3+j])
limit = max(abs(np.min(dens)), abs(np.max(dens)) )
im = ax[i,j].imshow(dens, origin='lower', interpolation='bilinear',
extent=[-2,2,-2,2], cmap='PiYG', vmin=-limit, vmax=limit)
ax[i,j].set_xlabel('Distance a.u.')
ax[i,j].set_ylabel('Distance a.u.')
divider = make_axes_locatable(ax[i,j])
cax = divider.append_axes('right', size='5%', pad=0.05)
fig.colorbar(im, cax=cax, orientation='vertical')
def calculate_co():
mol = Molecule()
mol.add_atom('C', 0.0, -0.5, 0.0)
mol.add_atom('O', 0.0, 0.5, 0.0)
result = HF().rhf(mol, 'sto3g')
return result['cgfs'], result['orbc']
def plot_wavefunction(cgfs, coeff):
# build integrator
integrator = PyQInt()
# build grid
x = np.linspace(-2, 2, 100)
y = np.linspace(-2, 2, 100)
xx, yy = np.meshgrid(x,y)
zz = np.zeros(len(x) * len(y))
grid = np.vstack([xx.flatten(), yy.flatten(), zz]).reshape(3,-1).T
res = integrator.plot_wavefunction(grid, coeff, cgfs).reshape((len(y), len(x)))
return res
if __name__ == '__main__':
main()
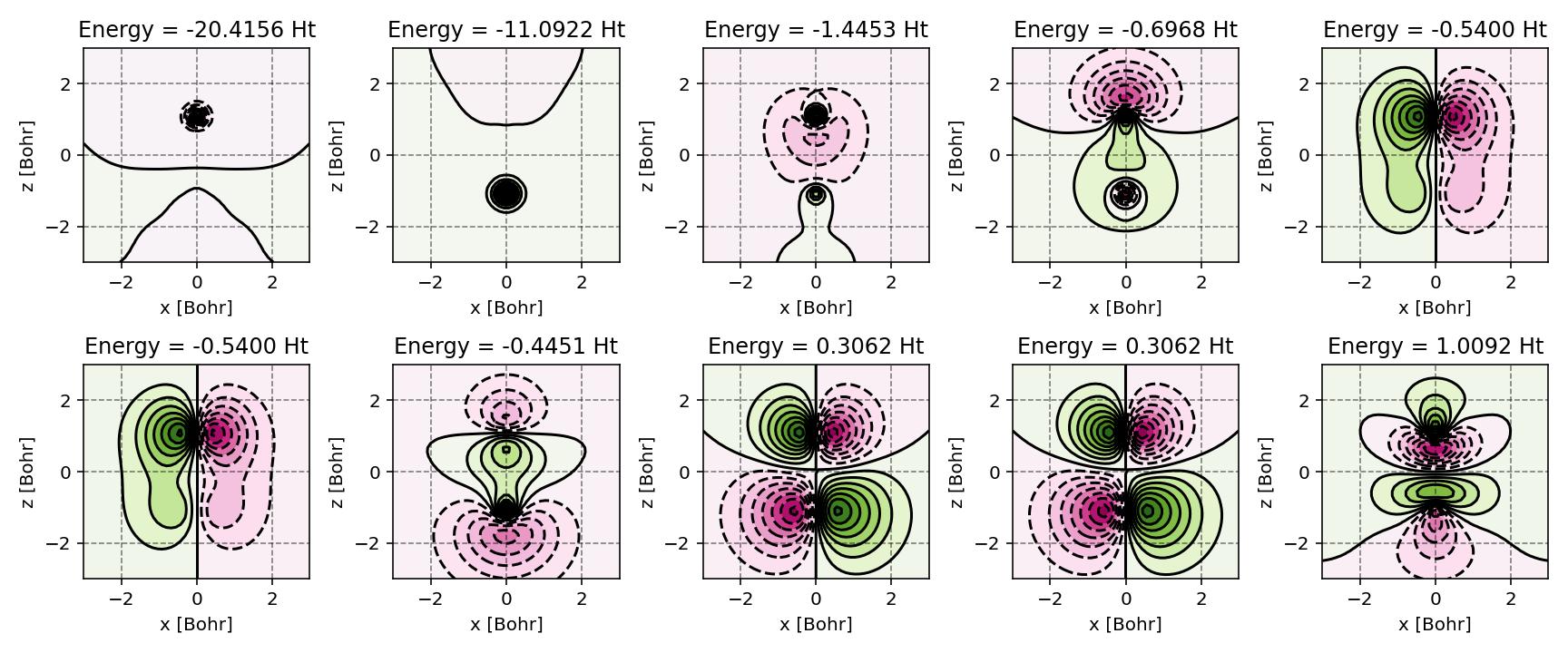
Canonical molecular orbitals of CO visualized using contour plots.
Result dictionary
The result of a Hartree-Fock calculation is captured inside a dictionary object. This dictionary objects contains the following keys
Key |
Description |
|---|---|
|
Final energy of the electronic structure calculation |
|
List of elements and their position in Bohr units |
|
List of contracted Gaussian functional objects |
|
List of energies during the self-convergence procedure |
|
Orbital energies (converged) (array of N element) |
|
Orbital coefficients (converted) (matrix of N x N elements) |
|
Density matrix \(\mathbf{P}\) |
|
Fock matrix \(\mathbf{F}\) |
|
Unitary transformation matrix \(\mathbf{X}\) |
|
Overlap matrix \(\mathbf{S}\) |
|
Kinetic energy matrix \(\mathbf{T}\) |
|
Nuclear attraction matrix \(\mathbf{V}\) |
|
Core Hamiltonian matrix \(\mathbf{H_\textrm{core}}\) |
|
Two-electron tensor object \((i,j,k,l)\) |
|
Time statistics object |
|
Sum of kinetic and nuclear attraction energy |
|
Total kinetic energy |
|
Total nuclear attraction energy |
|
Total electron-electron repulsion energy |
|
Total exchange energy |
|
Electrostatic repulsion energy of the nuclei |
|
Total number of electrons |
|
Forces on the atoms (if calculated, else |
To provide an example how one can use the above data, let us consider the situation wherein the user wants to decompose the individual components of the total energy as given by
Via the script below, one can easily verify that the above equation holds and that the total energy is indeed the sum of the kinetic, nuclear attraction, electron-electron repulsion, exchange and nuclear repulsion energies within a Hartree-Fock calculation.
from pyqint import MoleculeBuilder,HF
mol = MoleculeBuilder().from_name('ch4')
mol.name = 'CH4'
res = HF().rhf(mol, 'sto3g')
print()
print('Kinetic energy: ', res['ekin'])
print('Nuclear attraction energy: ', res['enuc'])
print('Electron-electron repulsion: ', res['erep'])
print('Exchange energy: ', res['ex'])
print('Repulsion between nuclei: ', res['enucrep'])
print()
print('Total energy: ', res['energy'])
print('Sum of the individual terms: ',
res['ekin'] + res['enuc'] + res['erep'] + res['ex'] + res['enucrep'])
The output of the above script yields:
Kinetic energy: 39.42613774982387
Nuclear attraction energy: -118.63789179775034
Electron-electron repulsion: 32.7324270326041
Exchange energy: -6.609004673631048
Repulsion between nuclei: 13.362026647057352
Total energy: -39.72630504189621
Sum of the individual terms: -39.726305041896055
Custom basis sets
Besides the basis sets offered by PyQInt, one can also use a custom
basis set defined by the user. The rhf routine accepts either a basis set
for its basis argument, or alternatively a list of cgf objects.
In the example code shown below, the latter is done.
mol = Molecule()
mol.add_atom('H', 0.0000, 0.0000, 0.3561150187, unit='angstrom')
mol.add_atom('H', 0.0000, 0.0000, -0.3561150187, unit='angstrom')
nuclei = mol.get_nuclei()
cgfs = []
for n in nuclei:
_cgf = cgf(n[0])
_cgf.add_gto(0.154329, 3.425251, 0, 0, 0)
_cgf.add_gto(0.535328, 0.623914, 0, 0, 0)
_cgf.add_gto(0.444635, 0.168855, 0, 0, 0)
cgfs.append(_cgf)
res = HF().rhf(mol, basis=cgfs)
Hint
A nice website to find a large collection of Gaussian Type basis set coefficients is https://www.basissetexchange.org/.
Orbital visualization
Since orbitals are essentially three-dimensional scalar fields, there are two useful procedures to visualize them. The scalar field can either be projected onto a plane, creating so-called contour plots. Alternatively, a specific value (i.e. the isovalue) of the scalar field can be chosen and all points in space that have this value can be tied together creating a so-called isosurface.
Contour plots can be easily created using matplotlib. For the creation of isosurfaces, we use PyTessel.
Contour plots
from pyqint import PyQInt, Molecule
import matplotlib.pyplot as plt
import numpy as np
# coefficients (calculated by Hartree-Fock using a sto3g basis set)
coeff = [8.37612e-17, -2.73592e-16, -0.713011, -1.8627e-17, 9.53496e-17, -0.379323, 0.379323]
# construct integrator object
integrator = PyQInt()
# build water molecule
mol = Molecule('H2O')
mol.add_atom('O', 0.0, 0.0, 0.0)
mol.add_atom('H', 0.7570, 0.5860, 0.0)
mol.add_atom('H', -0.7570, 0.5860, 0.0)
cgfs, nuclei = mol.build_basis('sto3g')
# build grid
x = np.linspace(-2, 2, 50)
y = np.linspace(-2, 2, 50)
xx, yy = np.meshgrid(x,y)
zz = np.zeros(len(x) * len(y))
grid = np.vstack([xx.flatten(), yy.flatten(), zz]).reshape(3,-1).T
res = integrator.plot_wavefunction(grid, coeff, cgfs).reshape((len(y), len(x)))
# plot wave function
plt.imshow(res, origin='lower', extent=[-2,2,-2,2], cmap='PiYG')
plt.colorbar()
plt.title('1b$_{2}$ Molecular orbital of H$_{2}$O')
Constructing isosurfaces
Note
Isosurface generation requires the PyTessel package to be installed. More information can be found here.
from pyqint import PyQInt, Molecule, HF
import numpy as np
from pytessel import PyTessel
def main():
# calculate sto3g coefficients for h2o
cgfs, coeff = calculate_co()
# build isosurface of the fifth MO
# isovalue = 0.1
# store result as .ply file
build_isosurface('co_04.ply', cgfs, coeff[:,4], 0.1)
def build_isosurface(filename, cgfs, coeff, isovalue):
# generate some data
sz = 100
integrator = PyQInt()
grid = integrator.build_rectgrid3d(-5, 5, sz)
scalarfield = np.reshape(integrator.plot_wavefunction(grid, coeff, cgfs), (sz, sz, sz))
unitcell = np.diag(np.ones(3) * 10.0)
pytessel = PyTessel()
vertices, normals, indices = pytessel.marching_cubes(scalarfield.flatten(), scalarfield.shape, unitcell.flatten(), isovalue)
pytessel.write_ply(filename, vertices, normals, indices)
def calculate_co():
mol = Molecule()
mol.add_atom('C', 0.0, -0.5, 0.0)
mol.add_atom('O', 0.0, 0.5, 0.0)
result = HF().rhf(mol, 'sto3g')
return result['cgfs'], result['orbc']
if __name__ == '__main__':
main()
Orbital localization: Foster-Boys
Background of FB
The canonical orbitals of a Hartree-Fock calculation are defined such that these will diagonalize the Fock-matrix by which these molecular orbitals are eigenfunctions of the Fock-operator. Nevertheless, this set of solutions is not unique in the sense that multiple sets of molecular orbitals produce the same electron density and the same total electronic energy. One is allowed to perform an arbitrary unitary transformations on the set of occupied orbitals yielding a new set that is as good as a representation as the old set. Some of these representations are however more useful than others and one particular useful representation is the one that makes the orbitals as localized (compact and condensed) as possible.
The degree of localization can be captured via relatively simple metric as given by
where \(\psi_{i}\) is a molecular orbital and \(i\) loops over the occupied
molecular orbitals. One obtains (perhaps counter-intuitively) the most localized orbitals
by maximizing the value of mathcal{M}.
The process of mixing the molecular orbitals among themselves to the aim of maximizing
is mathcal{M} is embedded in the FosterBoys class.
Procedure of FB
The code below first performs a Hartree-Fock calculation on the CO molecule after which the localized molecular orbitals are calculated using the Foster-Boys method. The Foster-Boys localization procedure is present as a separate class in the PyQInt package. It takes the output of a Hartree-Fock calculation as its input.
Note
The code below uses the PyTessel package for constructing the isosurfaces. PyTessel is an external package for easy construction of isosurfaces from scalar fields. More information is given in the corresponding section.
from pyqint import Molecule, HF, PyQInt, FosterBoys
import pyqint
import numpy as np
from pytessel import PyTessel
def main():
res = calculate_co(1.145414)
resfb = FosterBoys(res).run()
for i in range(len(res['cgfs'])):
build_isosurface('MO_%03i' % (i+1),
res['cgfs'],
resfb['orbc'][:,i],
0.1)
def calculate_co(d):
"""
Full function for evaluation
"""
mol = Molecule()
mol.add_atom('C', 0.0, 0.0, -d/2, unit='angstrom')
mol.add_atom('O', 0.0, 0.0, d/2, unit='angstrom')
result = HF().rhf(mol, 'sto3g')
return result
def build_isosurface(filename, cgfs, coeff, isovalue, sz=5, npts=100):
# generate some data
isovalue = np.abs(isovalue)
integrator = PyQInt()
grid = integrator.build_rectgrid3d(-sz, sz, npts)
scalarfield = np.reshape(integrator.plot_wavefunction(grid, coeff, cgfs), (npts, npts, npts))
unitcell = np.diag(np.ones(3) * 2 * sz)
pytessel = PyTessel()
vertices, normals, indices = pytessel.marching_cubes(scalarfield.flatten(), scalarfield.shape, unitcell.flatten(), isovalue)
fname = filename + '_pos.ply'
pytessel.write_ply(fname, vertices, normals, indices)
vertices, normals, indices = pytessel.marching_cubes(scalarfield.flatten(), scalarfield.shape, unitcell.flatten(), -isovalue)
fname = filename + '_neg.ply'
pytessel.write_ply(fname, vertices, normals, indices)
if __name__ == '__main__':
main()
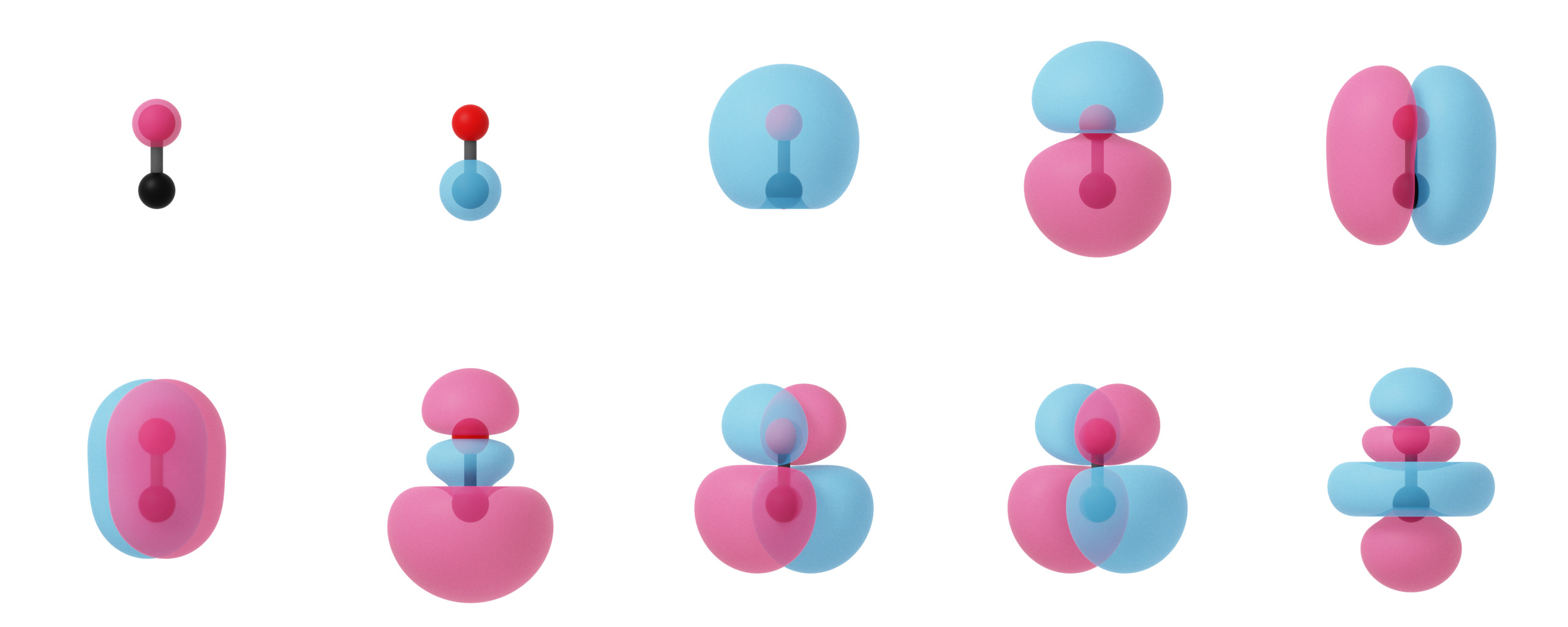
Canonical molecular orbitals of CO visualized using isosurfaces with an isovalue of +/-0.03.
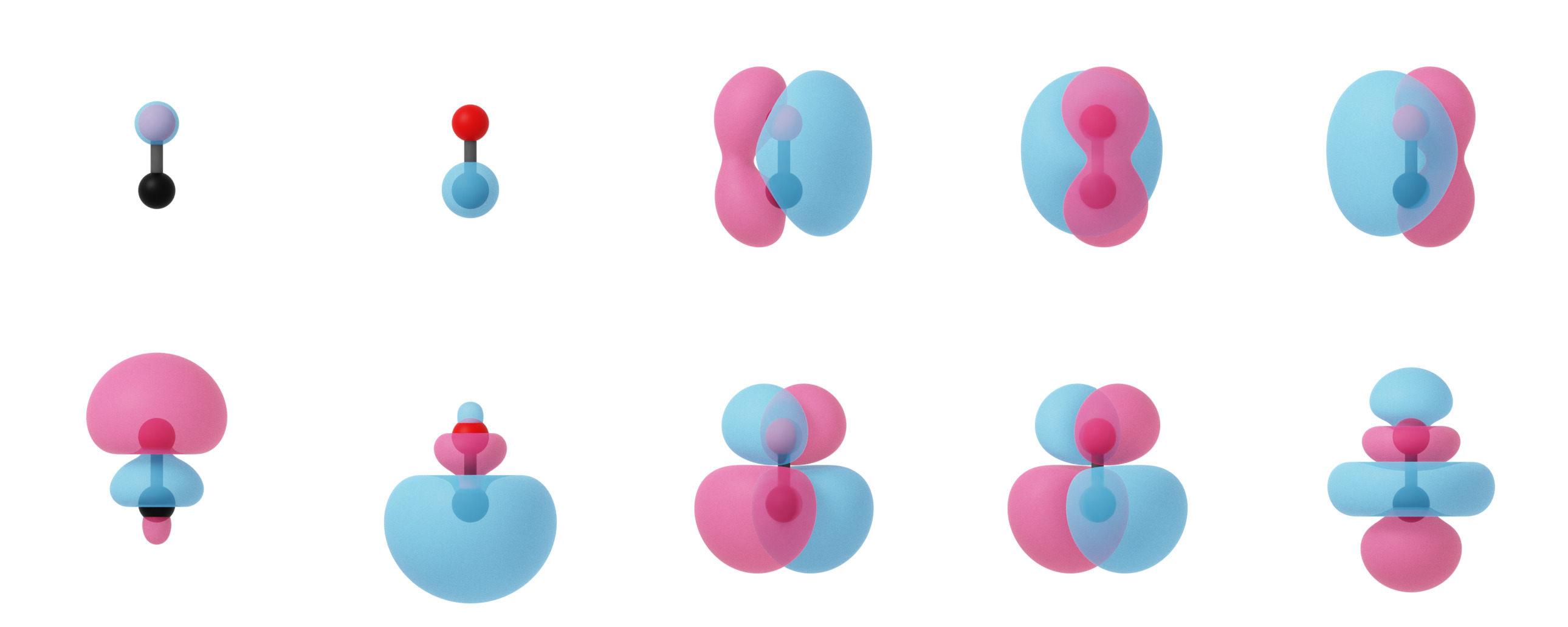
Localized molecular orbitals of CO visualized using isosurfaces with an isovalue of +/-0.03. Note that the localization procedure has only been applied to the occupied molecular orbitals. Observe that the localized orbitals contain a triple-degenerate state corresponding to the triple bond and two lone pairs for C and O.
Foster-Boys output object
The output object of a Foster-Boys calculation is very similar to the one of a Hartree-Fock calculation. It is a dictionary that contains the following elements.
Key |
Description |
|---|---|
|
Orbital energies after the unitary transformation. |
|
Orbital coefficient after the unitary transformation. |
|
Number of iterations. |
|
Initial sum of the squared dipole moment norm of the molecular orbitals. |
|
Final sum of the squared dipole moment norm of the molecular orbitals. |
Hint
One can directly connect the output of a Foster-Boys calculation to a COHP calculation. The details of the process are found in the cohp analysis of Foster-Boys localized orbitals section.
Geometry optimization
Performing a geometry optimization
PyQInt is able to perform a geometry optimization of a molecule. It
should however be noted that this functionality is rather limited and essentially
makes use of existing routines available in Scipy,
specifically the scipy.optimize.minimize routine using the
conjugate gradient method.
To demonstrate the procedure, let us consider the CH4 molecule in a non-converged geometry wherein the C-H bonds are longer than their optimal value and where the C molecule does not lie in the middle of the 4 hydrogen atoms.
Geometry optimization is handled by the GeometryOptimization class
which takes a molecule and a basis set as input. The user can indicate whether
they prefer verbose output or not. By default, geometry optimization is silent
and does not yield any output.
from pyqint import GeometryOptimization, Molecule
mol = Molecule()
dist = 1.0
mol.add_atom('C', 0.1, 0.0, 0.1, unit='angstrom')
mol.add_atom('H', dist, dist, dist, unit='angstrom')
mol.add_atom('H', -dist, -dist, dist, unit='angstrom')
mol.add_atom('H', -dist, dist, -dist, unit='angstrom')
mol.add_atom('H', dist, -dist, -dist, unit='angstrom')
res = GeometryOptimization(verbose=True).run(mol, 'sto3g')
The output of the above script (condensed) is:
================================================================================
START GEOMETRY OPTIMIZATION
USING CONJUGATE GRADIENT PROCEDURE
================================================================================
================================================================================
START GEOMETRY OPTIMIZATION STEP 001
================================================================================
-------------
POSITIONS
-------------
C 0.18897260 0.00000000 0.18897260
H 1.88972599 1.88972599 1.88972599
H -1.88972599 -1.88972599 1.88972599
H -1.88972599 1.88972599 -1.88972599
H 1.88972599 -1.88972599 -1.88972599
------------
ENERGIES
------------
Kinetic: 39.25312907
Nuclear: -108.88176703
Electron-electron repulsion: 28.15079420
Exchange: -6.09926187
Nuclear repulsion: 8.45508042
TOTAL: -39.12202522
----------
FORCES
----------
C 3.1181e-02 4.3241e-04 3.1181e-02
H 8.2117e-02 9.6104e-02 8.2117e-02
H -9.8833e-02 -8.6370e-02 7.3271e-02
H -8.7735e-02 7.6203e-02 -8.7735e-02
H 7.3271e-02 -8.6370e-02 -9.8833e-02
================================================================================
END GEOMETRY OPTIMIZATION STEP 001
================================================================================
================================================================================
START GEOMETRY OPTIMIZATION STEP 002
================================================================================
-------------
POSITIONS
-------------
C 0.15779172 -0.00043241 0.15779172
H 1.80760940 1.79362217 1.80760940
H -1.79089261 -1.80335642 1.81645509
H -1.80199100 1.81352308 -1.80199100
H 1.81645509 -1.80335642 -1.79089261
------------
ENERGIES
------------
Kinetic: 39.15431742
Nuclear: -109.64154344
Electron-electron repulsion: 28.55700060
Exchange: -6.14351258
Nuclear repulsion: 8.85933366
TOTAL: -39.21440434
----------
FORCES
----------
C 2.9218e-02 1.2969e-03 2.9218e-02
H 8.3762e-02 9.5182e-02 8.3762e-02
H -9.9519e-02 -8.8931e-02 7.7954e-02
H -9.1414e-02 8.1383e-02 -9.1414e-02
H 7.7954e-02 -8.8931e-02 -9.9519e-02
================================================================================
END GEOMETRY OPTIMIZATION STEP 002
================================================================================
...
================================================================================
START GEOMETRY OPTIMIZATION STEP 023
================================================================================
-------------
POSITIONS
-------------
C 0.03778625 -0.00000429 0.03778625
H 1.21921718 1.18193814 1.21921718
H -1.14362357 -1.18156895 1.21959236
H -1.14399962 1.18120405 -1.14399962
H 1.21959236 -1.18156895 -1.14362357
------------
ENERGIES
------------
Kinetic: 39.46557443
Nuclear: -118.95707554
Electron-electron repulsion: 32.86555691
Exchange: -6.62308238
Nuclear repulsion: 13.52216307
TOTAL: -39.72686352
----------
FORCES
----------
C -6.5246e-06 -4.8303e-06 -6.5246e-06
H 2.1794e-06 -3.7479e-06 2.1795e-06
H 2.6888e-06 7.3055e-06 -5.7105e-07
H 2.2273e-06 -6.0329e-06 2.2273e-06
H -5.7103e-07 7.3056e-06 2.6888e-06
================================================================================
END GEOMETRY OPTIMIZATION STEP 023
================================================================================
Result dictionary of a geometry optimization
The result of a Geometry Optimization calculation is captured inside a dictionary object. This dictionary objects contains the following keys
Key |
Description |
|---|---|
|
|
|
List of the total electronic energy at each ionic step. |
|
List of the forces on all the atoms at each ionic step. |
|
Coordinates of the atoms at each ionic step. |
|
Result dictionary of the Hartree-Fock calculation last ionic step. |
To demonstrate the use of the above data, consider the script as shown below.
In this script, we generate a CH4 in a (highly) perturbed configuration.
The perturbed configuration is generated using a random number generator (RNG). For
reproduction purposes, we have seeded this RNG such that the result as shown
below can be easily reproduced. The result of the geometry optimization is
captured in the res variable which is a dictionary according to the
above-mentioned specifications.
To show how the contents of this dictionary can be used, we produce two plots which are explained below.
from pyqint import GeometryOptimization, Molecule
import matplotlib.pyplot as plt
import numpy as np
# seed the random number generator to yield reproducible result
np.random.seed(4)
# build a CH4 molecule where the atom positions are perturbed based on a
# random number generator
mol = Molecule()
dist = 1.0
mol.add_atom('C', 0.1, 0.0, 0.1, unit='angstrom')
mol.add_atom('H', dist + np.random.rand(),
dist + np.random.rand(),
dist + np.random.rand(),
unit='angstrom')
mol.add_atom('H', -dist + np.random.rand(),
-dist + np.random.rand(),
dist + np.random.rand(),
unit='angstrom')
mol.add_atom('H', -dist + np.random.rand(),
dist + np.random.rand(),
-dist + np.random.rand(),
unit='angstrom')
mol.add_atom('H', dist + np.random.rand(),
-dist + np.random.rand(),
-dist + np.random.rand(),
unit='angstrom')
# perform the geometry optimization
res = GeometryOptimization(verbose=False).run(mol, 'sto3g')
# collect the RMS of the force
rms = np.zeros(len(res['coordinates']))
for i in range(len(res['coordinates'])):
forces = res['forces'][i]
rms[i] = np.sqrt(np.sum(np.linalg.norm(forces, axis=0) / float(len(forces))))
# plot electronic energy and RMS of the force
fig, ax1 = plt.subplots(dpi=144, figsize=(6,4))
ax1.plot(res['energies'], '-o', color='black')
ax2 = plt.twinx()
ax2.plot(rms, '-o', color='red')
ax2.set_ylabel('Root-mean-square force')
ax2.tick_params(axis='y', colors='red')
ax2.yaxis.label.set_color('red')
ax2.spines['right'].set_color('red')
ax1.grid(linestyle='--', color='black', alpha=0.5)
ax1.set_xlabel('Iteration [-]')
ax1.set_ylabel('Electronic energy [Ht]')
plt.tight_layout()
plt.show()
# show convergence of C-H bond distances for all bonds
# collect data
distances = np.zeros((4, len(res['coordinates'])))
for i in range(0,4):
for j in range(0, len(res['coordinates'])):
coord = res['coordinates'][j]
distances[i,j] = np.linalg.norm(coord[i+1] - coord[0])
# plot in a figure
plt.figure(dpi=144, figsize=(6,4))
for i in range(0,4):
plt.plot(distances[i,:], '-o', alpha=0.5, label='H$_{%i}$' % (i+1))
plt.grid(linestyle='--', color='black', alpha=0.5)
plt.xlabel('Iteration [-]')
plt.ylabel('C-H bond distance [Bohr]')
plt.legend(loc='right')
plt.tight_layout()
plt.show()
The result of the above script are the following two images, showcasing the optimization procedure and an example application of the data in the result dictionary. The first figure shows the total electronic energy and the root-mean-square of the force as function of the iteration number. The convergence criterion is essentially such that these forces need to be smaller than a threshold value. From the figure, it is clear that the total electronic energy converges faster than the forces.
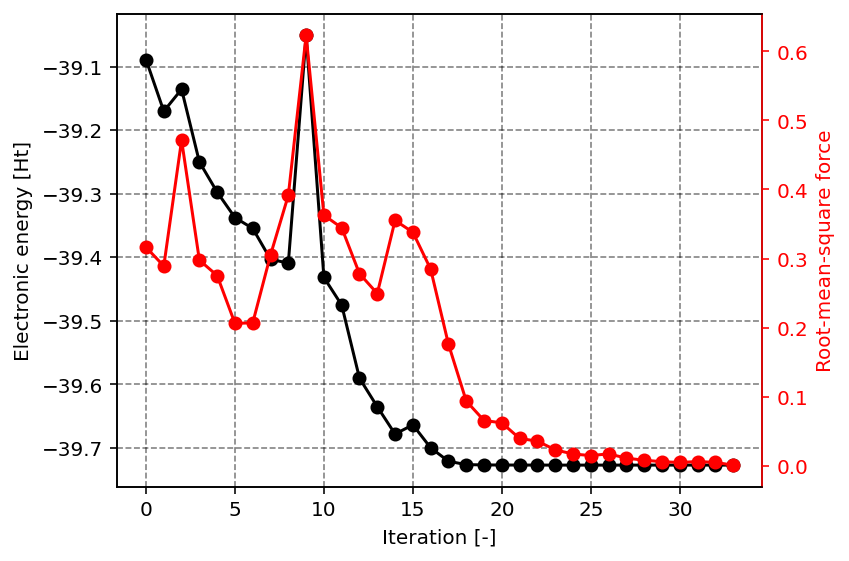
Energy and root-mean-square of the forces as function of the iteration number.
In the second figure, we can observe the C-H bond distance as function of the iteration number. Clearly, we start at a relatively unfavorable geometry where one of the H atoms is quite distanced from the central C atom. With increasing iteration, we can however readily see that all C-H bond distances converge to the same value, as expected for the highly symmetric CH4 molecule.
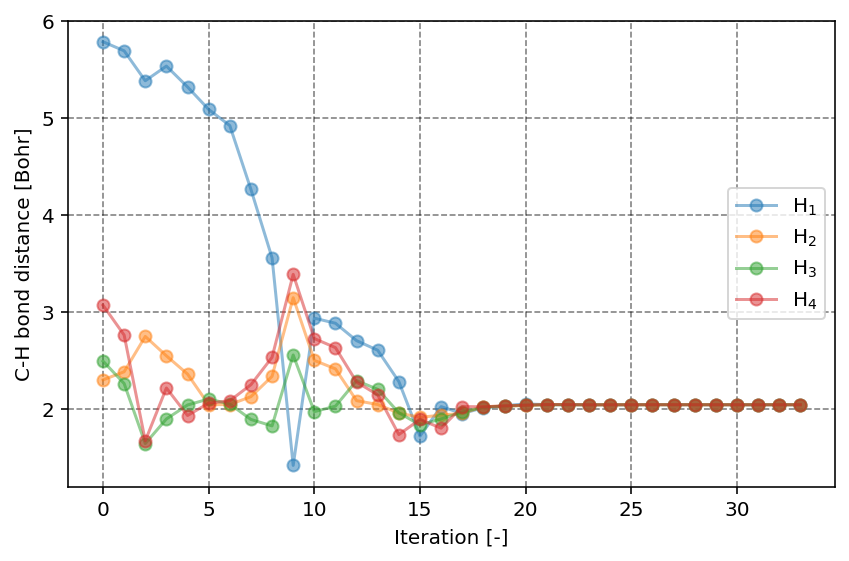
C-H bond distances as function of the iteration number.
Danger
It is by no means guaranteed that a geometry optimization converges. Even more important, when the geometry optimization has not converged, it is also highly likely that the underlying electronic structure calculation has not been properly converged as well. One should absolutely distrust any result coming out of such a calculation.
Always verify that a calculation is properly converged before using its output.
Crystal Orbital Hamilton Population Analysis
Background of COHP
Within the scope of chemical bonding, we can classify molecular orbitals to be bonding, anti-bonding or non-bonding with respect to any pair of atoms. When working with localized basis functions, the process of capturing the bonding character of the molecular orbitals is relatively straightforward as we can assign the basis functions constituting the molecular orbitals to an atom.
Within the framework of localized orbitals, the COHP coefficient of a given molecular orbital (\(\chi\)) is therefore defined as
where \(C_{ki}\) and \(C_{kj}\) are elements of the coefficient matrix \(\mathbf{C}\), \(H_{ij}\) an element of the Hamiltonian (Fock) matrix \(\mathbf{H}\) and \(\eta_{k}\) is the occupancy factor of molecular orbital \(k\) which is always 2 within a restricted Hartree-Fock calculation.
Note
It is perfectly possible to apply the above equation for unoccupied (virtual) orbitals, however the result should be interpreted from the perspective that such orbitals are merely artifacts of the diagonalization process as these orbitals do not correspond to any electron of the system.
Procedure of COHP
To perform a COHP calculation, one can direct the output of a Hartree-Fock calculation directly to the COHP class as demonstrated using the script below.
from pyqint import Molecule, HF, COHP, FosterBoys
d = 1.145414
mol = Molecule()
mol.add_atom('C', 0.0, 0.0, -d/2, unit='angstrom')
mol.add_atom('O', 0.0, 0.0, d/2, unit='angstrom')
res = HF().rhf(mol, 'sto3g')
cohp = COHP(res).run(res['orbc'], 0, 1)
print('COHP values of canonical Hartree-Fock orbitals')
for i,(e,chi) in enumerate(zip(res['orbe'], cohp)):
print('%3i %12.4f %12.4f' % (i+1,e,chi))
print()
The output of the above script is:
COHP values of canonical Hartree-Fock orbitals
1 -20.4156 0.0399
2 -11.0922 0.0104
3 -1.4453 -0.4365
4 -0.6968 0.2051
5 -0.5400 -0.2918
6 -0.5400 -0.2918
7 -0.4451 0.1098
8 0.3062 0.5029
9 0.3062 0.5029
10 1.0092 6.4828
COHP analysis of the Foster-Boys localized orbitals
It can be quite interesting to perform the COHP analysis on the Foster-Boys localized orbitals. The procedure is remarkably simple as the output of a Foster-Boys localization is very similar to the output of a Hartree-Fock calculation and one can direct the output of the former to the COHP class in the same manner.
In the script below, a Foster-Boys localization procedure is performed on the canonical Hartree-Fock orbitals of CO and on both results, a COHP analysis is performed, which can be readily compared.
from pyqint import Molecule, HF, COHP, FosterBoys
import numpy as np
d = 1.145414
mol = Molecule()
mol.add_atom('C', 0.0, 0.0, -d/2, unit='angstrom')
mol.add_atom('O', 0.0, 0.0, d/2, unit='angstrom')
res = HF().rhf(mol, 'sto3g')
cohp = COHP(res).run(res['orbc'], 0, 1)
resfb = FosterBoys(res).run()
cohp_fb = COHP(res).run(resfb['orbc'], 0, 1)
print('COHP values of canonical Hartree-Fock orbitals')
for i,(e,chi) in enumerate(zip(res['orbe'], cohp)):
print('%3i %12.4f %12.4f' % (i+1,e,chi))
print()
print('COHP values after Foster-Boys localization')
for i,(e,chi) in enumerate(zip(resfb['orbe'], cohp_fb)):
print('%3i %12.4f %12.4f' % (i+1,e,chi))
print()
print('Sum of COHP coefficient canonical orbitals: ', np.sum(cohp[:7]))
print('Sum of COHP coefficient Foster-Boys orbitals: ', np.sum(cohp_fb[:7]))
The output of the above script is:
COHP values of canonical Hartree-Fock orbitals
1 -20.4156 0.0399
2 -11.0922 0.0104
3 -1.4453 -0.4365
4 -0.6968 0.2051
5 -0.5400 -0.2918
6 -0.5400 -0.2918
7 -0.4451 0.1098
8 0.3062 0.5029
9 0.3062 0.5029
10 1.0092 6.4828
COHP values after Foster-Boys localization
1 -20.3075 0.0701
2 -11.0370 0.0450
3 -0.8309 -0.4092
4 -0.8309 -0.4092
5 -0.8309 -0.4092
6 -0.8137 0.2783
7 -0.5241 0.1792
8 0.3062 0.5029
9 0.3062 0.5029
10 1.0092 6.4828
Sum of COHP coefficient canonical orbitals: -0.6549007057824876
Sum of COHP coefficient Foster-Boys orbitals: -0.654900705782488
The results as shown above clearly demonstrate that not only the total energy and the electron density is invariant under a unitary transformation of the occupied molecular orbitals, also the sum of the COHP coefficient is an invariant. In other words, the (overall) bonding characteristics of the molecule remain the same under a unitary transformation.